.md .pdf

Contents

NP Complete

The Boolean SAT problem is exceptionally important to Computer Science. It is one of the problems in a class of problems known as NP-Complete. We will explain what that terminology means later in this section. In short, Boolean SAT is one of the hardest problems in Computer Science. It is also exactly as hard as many other important problems.

Comparing Problem Difficulty

How do we compare the difficulty of solving problems? Is sorting harder or easier than find the minimum? How could we know?

The key to comparing problem difficulty is to determine if having the solution to one problem can solve another problem.

Imagine we are given a random list of integers \(L\). What is harder, to sort the list or find the minimum?

We need to ask two questions.

1. If we sort the list, can we find the minimum trivially?

2. If we find the minimum of a list, can we trivially sort it?

The answer to the first question is yes. If we sort a list, we can trivially find the minimum. It will be the first element in the sorted list. The answer to the second question is no. If we know the minimum, we still don’t know anything about the rest of the elements. We would still have a lot of work ahead of us to sort the list.

We can conclude sorting is at least as hard as finding the minimum. Since sorting makes finding the minimum trivial, it cannot be easier than finding the minimum. It has to be equal or harder.

We can also conclude finding the minimum is easier than sorting. Finding the minimum did not make sorting a trivial problem. More work was needed. That means finding the minimum must be easier than sorting.

The key comparison is (Problem 1) is at least as hard as (Problem 2). We can decide this by determining that Problem 1 can make solving Problem 2 trivial. If we can figure this out, then we can solve Problem 2 my just going a few simple steps.

For example, we can write a findMin algorithm using sorting.

def findMin(L):
    L.sort()
    return L[0]

Any problem related to finding the minimum can always be solved if we have an algorithm for sorting. We might be able to do better. In this case we absolutely can write a better algorithm, but sorting is at least as hard as finding the minimum.

What happens if we can show two statements:

1. Problem 1 is at least as hard as Problem 2

2. Problem 2 is at least as hard as Problem 1

If we can show both of these, then we have shown that both problems are of the same difficulty level. If you could write an algorithm to solve either one of the problems, your algorithm trivially solves the other problem.

In the previous section, we showed that SAT is at least as hard as N-Queens. Having a SAT solver makes it easy to solve instances of the N-Queens problem.

Coloring SAT

The 3-Coloring Problem

A graph is an important data structure. We will only look at graphs visually in this section, not their implementation details.

A simple graph is shown below.

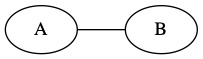
The graph is made up of nodes and edges. A node is a circle. We labeled the nodes by putting letter in this. This is not a requirement, but it makes the graph easier to talk about. There are two nodes, A and B.

A graph also has edges. An edge is a relationship between two nodes. It is drawn as a line connecting the two nodes.

The 3-Coloring Problem asks us to color a graph using exactly three colors such that no two nodes of the same color are connected by an edge. The following graph is a little more complicated.

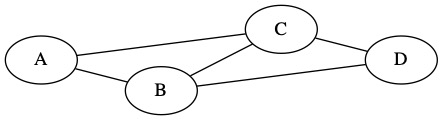
The specific three colors we want don’t really matter. We will pick: blue, yellow, and red. We can try coloring A red, B yellow, C yellow, and D blue.

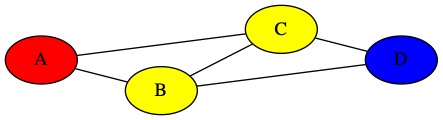
This is not a valid coloring. There is an edge connecting B and C, but they are both yellow. This is not allowed. If two nodes are connected by an edge, they cannot be the same color.

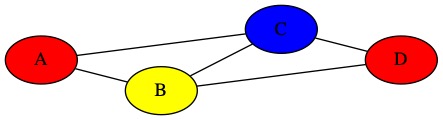
We can try a different coloring. This time we make A and D red, B yellow, and C blue. This does not break any rules.

This problem can be solved by a SAT solver. We create variables related to the nodes. We will create clauses related to the edges. Each node must be some color, we label variables based on the node and color. For example, \(A_{r}\) is true if node A is colored red.

Node A must have some color. This means \(A_{r} \vee A_{b} \vee A_{y}\). We don’t know which color, just that it will have one.

To say each node must be colored in, we write.

\( \begin{align} & \left( A_{r} \vee A_{b} \vee A_{y} \right) \\ & \wedge \left( B_{r} \vee B_{b} \vee B_{y} \right) \\ & \wedge \left( C_{r} \vee C_{b} \vee C_{y} \right) \\ & \wedge \left( D_{r} \vee D_{b} \vee D_{y} \right) \\ \end{align} \)

A node can’t be two colors. If node A is red, it can’t also be blue. More specifically, \(A_{r} \implies \neg A_{b}\). We need to add statements to ensure that no node has two colors.

\( \begin{align} & \wedge \left( \neg A_{r} \vee \neg A_{b} \right) \\ & \wedge \left( \neg A_{r} \vee \neg A_{y} \right) \\ & \wedge \left( \neg A_{b} \vee \neg A_{y} \right) \\ & \wedge \left( \neg B_{r} \vee \neg B_{b} \right) \\ & \wedge \left( \neg B_{r} \vee \neg B_{y} \right) \\ & \wedge \left( \neg B_{b} \vee \neg B_{y} \right) \\ & \wedge \left( \neg C_{r} \vee \neg C_{b} \right) \\ & \wedge \left( \neg C_{r} \vee \neg C_{y} \right) \\ & \wedge \left( \neg C_{b} \vee \neg C_{y} \right) \\ & \wedge \left( \neg D_{r} \vee \neg D_{b} \right) \\ & \wedge \left( \neg D_{r} \vee \neg D_{y} \right) \\ & \wedge \left( \neg D_{b} \vee \neg D_{y} \right) \end{align} \)

This is getting long a messy. We can use quantifier notations to shorten the expressions. Let \(N=\{A,B,C,D\}\) be the set of all nodes.

We need every node for have a color.

\( \begin{align} \forall X \in N \left( X_{r} \vee X_{b} \vee X_{y} \right) \end{align} \)

We need every node to have only one color.

\( \begin{align} \forall X \in N \left( (\neg X_{r} \vee \neg X_{b} ) \wedge (\neg X_{r} \vee \neg X_{y} ) \wedge (\neg X_{b} \vee \neg X_{y} ) \right) \end{align} \)

For each edge, we can’t have both sides being the same color. For example, node A and B are connected by an edge. If A is red, then B cannot be red. This is another condition \(A_{r} \implies \neg B_{r}\). Let \(E=\{ (A,B), (B,C), (A,C), (B,D), (C,D) \}\) be the set of all edges.

For all edges, the two sides cannot have the same color.

\( \begin{align} \forall (X,Y) \in E \left( ( \neg X_{r} \vee \neg Y_{r} ) \wedge ( \neg X_{y} \vee \neg Y_{y} ) \wedge ( \neg X_{b} \vee \neg Y_{b} ) \right) \end{align} \)

Putting it all together, we get an expression for the graph.

\( \begin{align} &\forall X \in N \left( (X_{r} \vee X_{b} \vee X_{y}) \wedge (\neg X_{r} \vee \neg X_{b} ) \wedge (\neg X_{r} \vee \neg X_{y} ) \wedge (\neg X_{b} \vee \neg X_{y} ) \right) \\ & \wedge \\ &\forall (X,Y) \in E \left( ( \neg X_{r} \vee \neg Y_{r} ) \wedge ( \neg X_{y} \vee \neg Y_{y} ) \wedge ( \neg X_{b} \vee \neg Y_{b} ) \right) \end{align} \)

A larger graph would require an algorithm approach to generate the DiMACs. We could still ask a SAT Solver how to solve it.

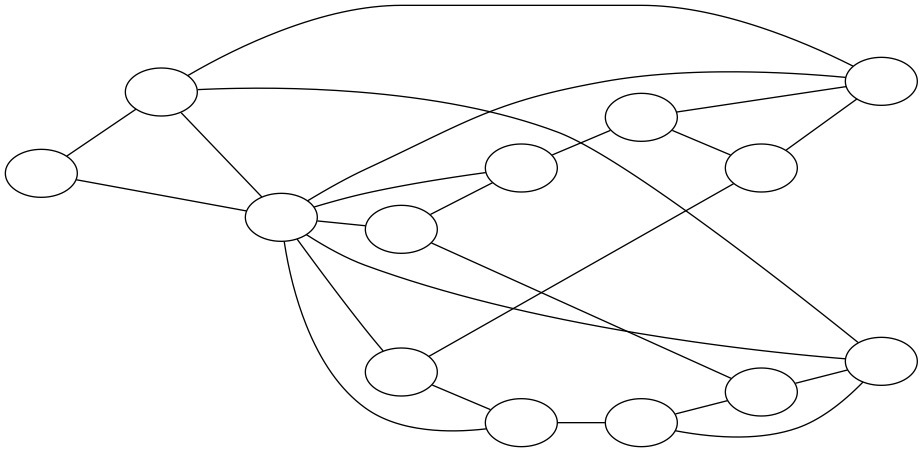
If we have a SAT Solver, we can solve any 3-Color problem. The SAT Problem is at least as hard as the three color problem.

Coloring as SAT

Imagine we had an amazing algorithm that could solve 3-color. Could we use it to solve SAT problems? Is 3-Color at least as hard as SAT.

Assume we have some CNF expression. We want to determine how to make it true. We can make an graph that can be colored if and only if the boolean expression is true. Further, the coloring of the graph will tell us the value of the SAT Problem.

We start with making our graph with a triangle. The every node in this triangle must have a different color.

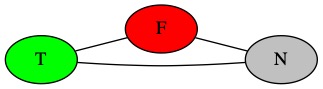
We pick one color to mean true and one to mean false. It doesn’t matter which color means which. It just matters which color gets colored. It doesn’t matter what color each of these nodes get, but whatever color it gets will mean something.

There are three nodes. Node T is for true. Node F is for False. Node N is none. This third node is needed for mechanical reasons. We need N to simulate the process of solving a SAT problem.

• T was green, so any green node is true

• F was red, so any red node is false

• N was grey, it only matters mechanically.

Any boolean expression has variables. We will build the expression \(X \iff Y\).

First, we simplify to CNF

\( \begin{align} &X \iff Y & \text{Premise} \\ &(X \implies Y) \wedge (Y \implies X) & \text{Def. of Bi-Conditional} \\ &(\neg X \vee Y) \wedge (\neg Y \vee X) & \text{Def. of Implies} \end{align} \)

We need all our variables to be either true or false. Also, we need \(X\) and \(\neg X\) to have opposite values.

We connect \(X\) and \(\neg X\) with an edge. They must have different colors. We also connect them both to \(N\). This ensures that one must be true and one must be false. We do the same with \(Y\) and \(\neg Y\).

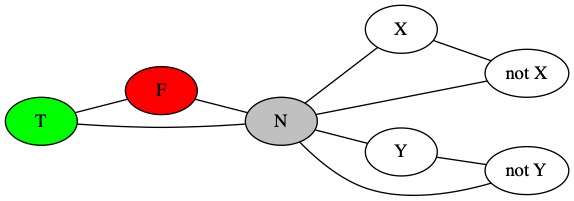
There are four ways to color this graph. Each represents a possible setting of the boolean variables. The edges to the N color ensure that only colors that also mean something in the truth table appear.

X Value	Y Value	X Color	not X Color	Y Color	not Y Color
True	True	Green	Red	Green	Red
True	False	Green	Red	Red	Green
False	True	Red	Green	Green	Red
False	False	Red	Green	Red	Green

We can use another triangle to create a disjunction. The triangle has two input nodes. They are linked to the variables we want to read as input. The third node of the triangle is the output. We connect it to both F and N. This means the result must be true.

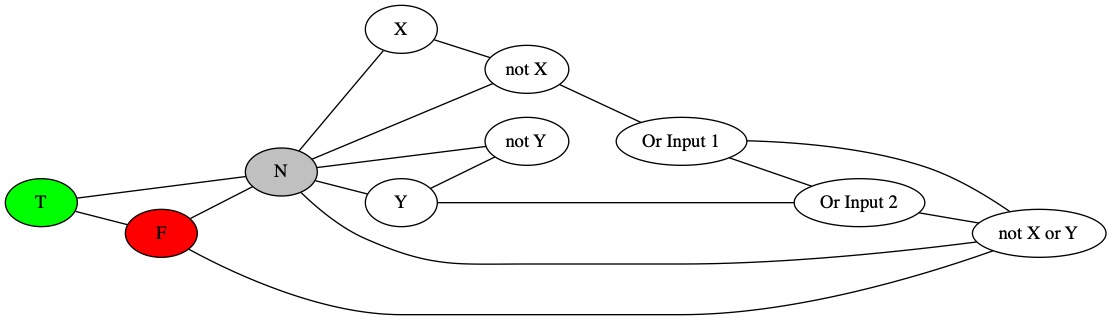
This graph represented \(\neg X \vee Y\). We know the truth table for this expression. It is given below.

Row	X	Y	\(\neg X \vee Y\)
1	True	True	True
2	True	False	False
3	False	True	True
4	False	False	True

The three true rows can be colored in.

Coloring for Row 1.

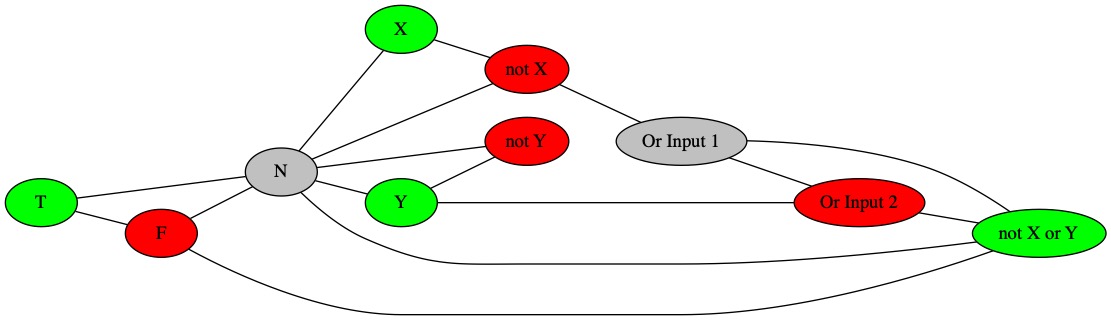
The Row 2 is false. It is impossible to color it in. There is no possible color for the last node.

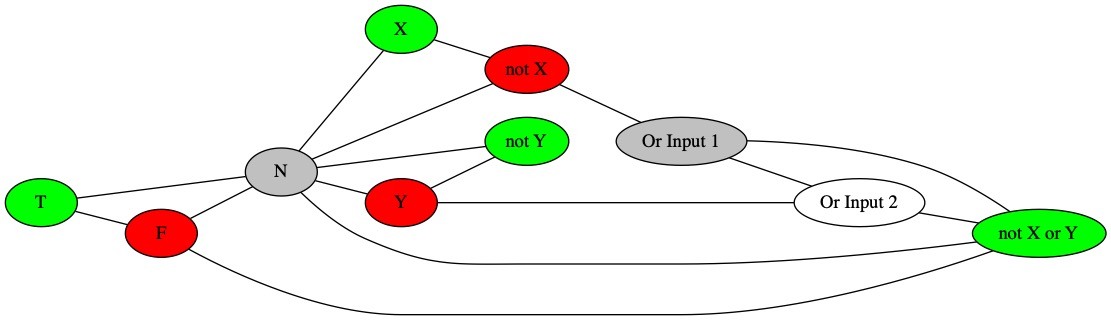
Coloring for Row 3.

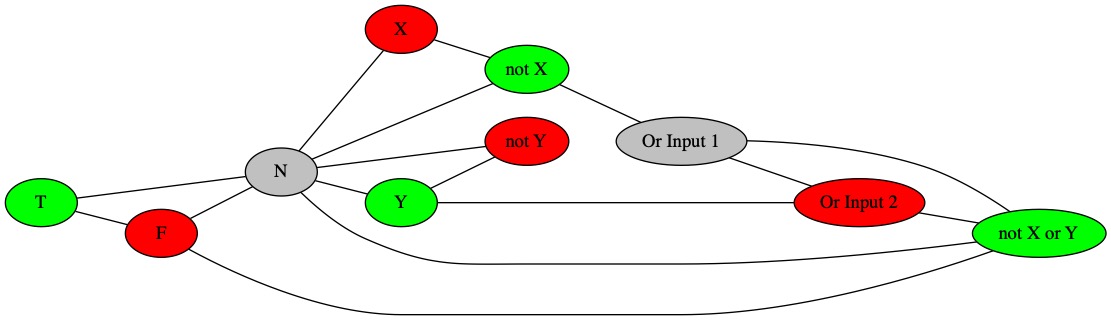
Coloring for Row 4.

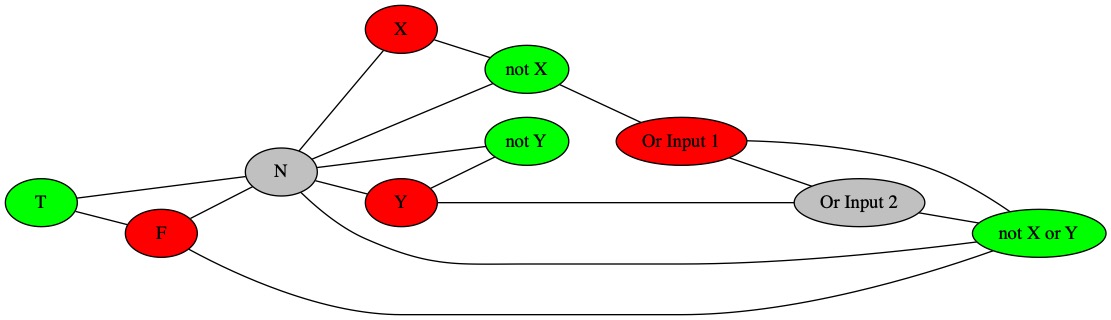
Our target question was \((\neg X \vee Y) \wedge (\neg Y \vee X)\). We need another disjunction. We can create the conjunction by just making sure the output of both disjunctions must be true.

The following is a completely uncolored graph for \((\neg X \vee Y) \wedge (\neg Y \vee X)\). We can ask a 3-Color algorithm to color this graph. Then we just need to look at the colors assigned to T, F, X, and Y to know the answer.

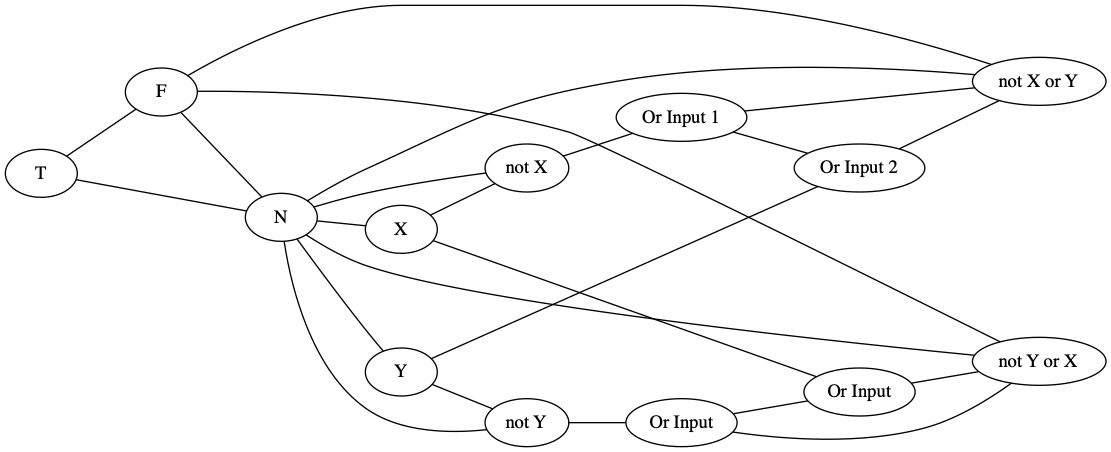
These steps can be generalized to any boolean expression in CNF form. We already know any boolean expression can be written as CNF. That means, we can turn any Boolean expression into a 3-Color Graph Problem.

We conclude that 3-Color is at least as hard as SAT.

SAT is 3-Color

We have shown that a SAT solver can solve any 3-color problem. We have also known that a 3-Color algorithm can solve any SAT problems. This shows the two problems have the same difficulty.

A fast algorithm for either of these problems can solve both of these problems.

Complexity Classes

We have terminology to classify problems. This gives us an easy why to talk about how hard a problem is.

The first class is called P. The P is for polynomial. This class includes any problem that can be solved with a polynomial amount of steps. The amount of steps the computer must complete to solve the problem and get the correct answer can be represented by a formula like \(a_{n}x^{n} + a_{n-1}x^{n-1} + \cdots a_{1}x + a_{0}\). Most algorithms you have ever written are probably in class P.

The next class is called NP. This class contains any problem that can be verified in polynomial time. Remember, verification means that we can check if an answer is correct. If we can verify and answer, there is one algorithm that will always solve the problem. That algorithm is BRUTE FORCE! We try every possible combination of inputs until we find the right one.

The letters NP stand for non-deterministic polynomial. A non-deterministic computer is a special imaginary machine. You have probably used computers with multiple processors. These computers can run many programs at the same time. A non-deterministic computer is an imaginary computer with infinite processors. It can brute force a problem by running one possible input on every one of its infinite processors.

Any problem in P can be solved by brute force, it would just be stupid to do. We have better algorithms. We can say that \(P \in NP\).

The critical question is, are their any questions that can only be solved by the brute force method. The answer to this question is currently unknown.

There are a few problems we currently cannot solve any way but trial and error. One of these problems is SAT. Any algorithm that is designed to solve the SAT problem must look at the entire truth table in the worse case. Not matter what optimizations or improvements are made, sometimes building the truth table is the only option. At least, as far as we know that is true.

The SAT problem is in a class called NP-Complete. These are problems that can only be solved by trying all combinations against a verification algorithm.

One important thing about NP-complete is every problem in it has an equivalent difficultly to SAT. If someone could solve SAT in polynomial time, they would also solve every other problem that is NP-Complete. They would also have proven that \(P=NP\). There would be no problems left in NP we couldn’t solve in polynomial time.

There is also a final even harder set of problems called NP-Hard. These include problems were we don’t even know how to verify answers quickly. These problems are important in cryptography. They form the basic for algorithms that we can use to build encryption.

We showed that SAT and 3-Color are equivalent difficulty problems. They are both NP-Complete. The k-Color problem is the same as 3-color, except the user can specify any number of colors \(k\). This problem is also in NP-Complete. It can solve both SAT and 3-Color.

Note

When we show two problems are both in NP-Complete we call it a reduction. The steps needed to transform one question into another and parse the answer must be in class P. Otherwise, they transformation is to complex to work. All our transformations are in class P.

Universities often need to schedule exams. There are a finite number of time slots available to run exams. Students need to take certain exams. A student cannot take two exams at the same time. This is called the Exam Scheduling Problem.

The Exam Scheduling Problem is also NP-Complete. More specifically, it is actually just a rewording of the k-Color Problem. We just need to imagine the following graph.

• Every Exam is a Node

• If a student is in two classes, they have an edge

• Every time slot is a color

The Exam Scheduling Problem is the same as the SAT problem. If you could solve one efficiently, you could solve both.

You can see a list of some NP-Complete problems on wikipedia. Every one of these problems is equivalent to the SAT problem. Efficient SAT solvers are also efficient solves for every one of these problems.

The Boolean Satisfiability problem sits at the heart of all NP-Complete problems. It has been studied formally since George Boole invented modern boolean algebra in 1847, and philosophers have studied it for centuries before without the formalities [Boo47]. We have still never found a good algorithm to solve these problems. Since it has been studied for so long, we are very doubtful an efficient algorithm will be found.

previous

SAT Solvers

next

References