Normal Forms#
A normal form is a selected representative from a set of equivalent expressions. We use normal forms to convey information in a consistent manner.
Look at the following three polynomial expressions.
\( \begin{align*} &3x^2+4x+7 \\ &7+3x^2+4x \\ &7x\left( \frac{3x}{7}+\frac{4}{7}+\frac{1}{x} \right) \end{align*} \)
Did you notice all three expressions are the same? The first two are just minor re-orderings, so they are easy to pick out. The third expression is noticeably harder to figure out.
We becomes used to seeing polynomials in the form \(a_n x^n + a_{n-1} x^{n-1}+\cdots+a_1 x + a_0\). When people write expressions like this, we can immediately figure out things about the polynomial, for example its highest exponent. This makes it much easier to work with.
All the expressions are the same, but we would rather use one of them. A normal form an expression that follows a specific set of rules to write out.
We could summarize our polynomial rules.
Expressions should have the form \(\sum_{i=n}^{0}\left( a_{i} x^{i} \right)\)
All values \(a_i\) should be constants.
Exponents should be sorted in decreasing order.
Any position where \(a_i\)=0 should be skipped.
If people follow these rules, then they write polynomials in our normal form. This makes it easier to communicate and write out the expressions.
Boolean Normal Forms#
There are three well established normal forms related to Boolean Expressions. We frequently need to communicate expressions between computer programs. Having a consistent set of normal forms makes this easier.
The three normal forms we will look at are
Negative Normal Form (NNF)
Conjunctive Normal Form (CNF)
Disjunctive Normal Form (DNF)
The rules for these normal forms use some new terminology.
Literal: a variable, constant, or negation of a variable.
Clause: literals or expressions connected by operators.
Disjunctive Clause: a clause created using a disjunction.
Conjunctive Clause: a clause created using a conjunction.
It is important to differential between literals and clauses. A literal is something that can be trivially evaluated. A clause requires all its input operands evaluated, then it needs to be evaluated.
We also talk about where in an operator appears. We use the words above and below in relation to operators. One operator is above another if it gets evaluated after. One operator is below another if it gets evaluated before.
Here is an example expression with multiple operators. No operators are duplicated to avoid confusion.
\( \begin{align} A \implies \left( B \vee (\neg C \wedge D) \right) \end{align} \)
This expression has four literals. They are \(A, B, \neg C, D\). Notice that \(\neg C\) is considered a literal. The negation is applied directly to the variable \(C\).
The conditional operator is above all other operators. It is the last thing that gets evaluated. The disjunction is above the conjunction operator but below the conditional. The conjunction is below both conditional and the disjunction, it is only above the negation.
If we write the expression out in Racket notation, the above/below quality becomes even more obvious.
(implies A (or B (and (not C) D)))
The code need to be evaluated from the inside out. The outermost expressions are above the inner expressions. The terminology comes from thinking of the expression as a tree.
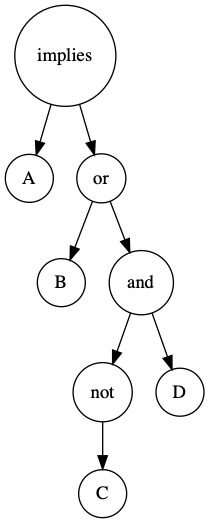
Using this terminology, we can define the three common normal forms.
Negative Normal Form#
The goal of Negative Normal Form (NNF) is to ensure there are no negations outside parenthesis. This is convenient because it means we want all clauses to be true.
We define NNF in terms of rules.
The negation symbol may only be applied to variables.
The only binary operators allowed are \(\vee\) and \(\wedge\).
Any expression that does not break these rules is in NNF. This means a trivial expression like \(A\) is in NNF. It has no negatives or operators, so it does not break any of the rules.
The following expressions are in NNF.
\( \begin{align} A \\ \neg A \vee \neg B \\ A \wedge B \end{align} \)
The following expressions are not in NNF.
\( \begin{align} \neg \neg A \\ \neg (A \vee B) \\ A \implies B \end{align} \)
The expression \(\neg \neg A\) breaks the first rule, a negation is applied to another negation. The expression \(\neg (A \vee B)\) also breaks the first rule. The negation is applied to the disjunction, not a variable. The last expression \(A \implies B\) breaks the third rule. It has an operator that is not allowed, the conditional.
We can write any boolean expression in NNF. We just need rules to replace bad expressions with equivalent good ones.
We can easily use the definitions of the conditional and bi-conditional to remove them.
\( \begin{align} A \iff B =& (A \implies B) \wedge (B \implies A) \\ A \implies B =& \neg A \vee B \end{align} \)
To remove any extra negations, we just need rules for now the negation interacts with the other operators. We can use DeMorgan’s law and double negative elimination.
\( \begin{align} \neg (A \vee B) =& \neg A \wedge \neg B \\ \neg (A \wedge B) =& \neg A \vee \neg B \\ \neg \neg A =& A \end{align} \)
These rules allows us to convert any Boolean Expression to NNF. If you wanted to use any other operators, like XOR, you would also need to add their definitions.
The NNF rules set is given in full below with names.
\( \begin{align} A \iff B =& (A \implies B) \wedge (B \implies A) &\text{Def. of Bi-Conditional} \\ A \implies B =& \neg A \vee B &\text{Def. of Conditional} \\ \neg (A \vee B) =& \neg A \wedge \neg B & \text{DeMorgan on Disjunction} \\ \neg (A \wedge B) =& \neg A \vee \neg B & \text{DeMorgan on Conjunction} \\ \neg \neg A =& A & \text{Double Negative Elimination} \end{align} \)
Any expression not in NNF can be converted into NNF by just applying these rules repeatedly.
The expression \(\neg(A \implies \neg B)\) has a negative in the wrong place and an illegal operator. We convert it to NNF.
\( \begin{align} &\neg (A \implies \neg B) & \text{Initial Expression} \\ &\neg ( \neg A \vee \neg B) & \text{Def. Of Conditional} \\ &\neg \neg A \wedge \neg \neg B & \text{DeMorgan on Disjunction} \\ &A \wedge B & \text{Double Negative Elimination} \end{align} \)
The normal form expression is written in a more consistent and easy to work with notation. The final expression is in NNF, it does not break any rules.
Conjunctive Normal Form#
The problem with NNF is that it doesn’t care about the disjunction or conjunction operators. This is inconvenient for many problems. We would like to know what to expect.
The goal of Conjunctive Normal Form (CNF) is to create one big conjunction statement.
A Boolean Expression is in CNF if it is a conjunction of one or more causes, where a clause is a disjunction of literals.
The rules of CNF are given below.
The expression must be in NNF.
All conjunctions must be above all disjunctions.
The following expressions are in CNF.
\( \begin{align} &(A \vee B) \wedge (\neg C \vee X \vee Q) \\ &A \vee X \\ &\neg A \wedge B \end{align} \)
The following are not in CNF. The reason why is given next to the expression.
\( \begin{align} &(\neg \neg A) \wedge B &\text{Not in NNF} \\ &A \vee (B \wedge C) &\text{OR above AND} \\ &B \wedge (C \vee (X \wedge B)) &\text{OR above AND} \end{align} \)
Any Boolean expression can be rewritten into CNF. First, we need to transform it into NNF. Then we need to apply one additional rule.
\( \begin{align} A \vee (X \wedge Y) =& (A \vee X) \wedge (A \vee Y) & \text{Disjunction Distribution} \end{align} \)
This rule can move any disjunction in an invalid location into a valid location.
We convert the expression \(\neg (A \wedge (B \vee C))\) into CNF form.
\( \begin{align} &\neg (A \wedge (B \vee C)) &\text{Initial Expression} \\ &\neg A \vee \neg( B \vee C) &\text{DeMorgan on Conjunction} \\ &\neg A \vee (\neg B \wedge \neg C) &\text{DeMorgan on Disjunction} \\ &(\neg A \vee \neg B) \wedge (\neg A \vee \neg C) &\text{Disjunction Distribution} \end{align} \)
In this case, the CNF expression was noticeably longer than the original. This will happen in many cases. Remember, our goal is consistency in how we write the expression.
Disjunctive Normal Form#
The Disjunctive Normal Form (DNF) is a flip of CNF. This time our goal is a big disjunction.
A Boolean Expression is in DNF if it is a disjunction of one or more clauses, where a clause is a conjunction of literals.
The rules for checking if an expression is in DNF are given below.
The expression must be in NNF.
All disjunctions must be above all conjunctions.
The following three examples are in DNF.
\( \begin{align} & (A \wedge X) \vee (B \wedge C) \\ & A \vee X \\ & \neg A \wedge B \end{align} \)
The following three are not in DNF. The reason they are not in DNF is given next to the expression.
\( \begin{align} & (A \vee B) \wedge (\neg C \vee X \vee Q) &\text{AND above OR} \\ & (\neg \neg A) \vee B &\text{Not in NNF}\\ & B \wedge (C \vee (X \wedge B)) &\text{AND above OR} \end{align} \)
Once an expression is in NNF, we only need one extra simplification rule to make it into DNF. We just need a different distribution law.
\( \begin{align} A \wedge (X \vee Y) =& (A \wedge X) \vee (A \wedge Y) &\text{Conjunction Distribution} \end{align} \)
We can transform any Boolean Expression in DNF form.
\( \begin{align} &\neg (A \vee (B \wedge C)) & \text{Initial Expression} \\ &\neg A \wedge \neg( B \wedge C) & \text{DeMorgan on Disjunction} \\ &\neg A \wedge (\neg B \vee \neg C) & \text{DeMorgan on Conjunction} \\ &(\neg A \wedge \neg B) \vee (\neg A \wedge \neg C) & \text{Conjunction Distribution} \end{align} \)
The CNF and DNF forms are both very consistent. Which ones it useful in any situation depends on the problem you are trying to solve.
DiMACS#
One of the most common questions related to Boolean Expression is “what setting of variables makes my expression true”. This is called the SAT problems. It is short for satisfiability. If it possible to come up with a setting of variables that will satisfy the expression by making it true. If it is possible, what is the setting of variables.
A SAT Solver is a program that is built to answers these questions as fast as possible. There are many companies and universities that create SAT Solvers. We have a special format for given them Boolean Expressions. It is a formalized version of CNF.
SAT Solvers are so popular that each year a competition is held to find the fastest solver. It is called the International SAT Competition. The first contest was held in 1992. In 2020, 48 different SAT solvers were entered into the main track. Additional solvers competed on secondary tracks designed for special purposes.
These programs are designed to work for expressions with millions of variables and clauses. They can be used to solve very complicated problems. One of the benchmarks in 2018 was to verify the accuracy of floating point calculations in a C program.
One of the long running competitors has been a program called CryptoMiniSAT. To get high levels or performance, this program needs to be installed and compiled for a specific system.
The developers also provide a simple javascript version that can be used for basic experiments. It can be run from this website.
This javascript version would be worthless in the International SAT Competition, but it is great for simple experiments.
Since all these solvers need to read expressions, we need a common language to write boolean expressions. This language is called DiMACs. It is a very formal version of CNF. It is designed to be exceptionally easy and efficient to parse.
A DiMACs file may have comments. A comment must take up an entire line. Comment lines always start with a c followed by a space. Then you can write whatever you want.
The DiMACs format starts with a problem statement. This is not required by all solvers, but some do require it. It is better to always provide it.
The problem statement looks like p cnf a b where a is the number of variables and b is the number of clauses. For example, if we had 3 variables and 4 clauses in cnf form, we would write p cnf 3 4. The p is short for problem.
Many solvers will also allow dnf to be used in the problem statement.
To make the file as easy to read as possible, the Boolean expression is written using numbers and formatting. Each variable is given a natural number \((1,2,3,\cdots)\). Zero has a special meaning and cannot be used as a variable.
To negate a variable, we apply the minus sign to the number. For example, -2 means apply a negation to variable two.
Each row in the file represents one disjunction of variables. The numbers are separated by spaces. The line must end in a 0. Zero is used as the “end of disjunction” character. The zero should be followed by a newline.
Every row of the file is then combined using a conjunction.
The following expression is already in CNF.
\( \begin{align} (\neg A \vee \neg B) \wedge (\neg C \vee X) \wedge C \end{align} \)
It has four variables. We will give each a number.
Variable |
Number |
|---|---|
A |
1 |
B |
2 |
C |
3 |
D |
4 |
The expression is made up of three clauses.
\( \begin{align} &(\neg A \vee \neg B) \\ &(\neg C \vee X) \\ &C \end{align} \)
Our problem statement is p cnf 4 3. We are writing a CNF expression with 4 variables and 3 clauses.
We need to write each clause in DiMACs.
Expression |
DiMACs |
|---|---|
\((\neg A \vee \neg B)\) |
|
\((\neg C \vee X)\) |
|
\(C\) |
|
We can put these all together into one DiMACs file. This would just be stored into a plain text file.
c (not A or not B) and (not C or X) and C
p cnf 4 3
-1 -2 0
-3 4 0
3 0
We can run this code in CryptoMiniSAT. It produces a lot of output, but the most important parts are at the bottom.
s SATISFIABLE
c ------- FINAL TOTAL SEARCH STATS ---------
c restarts : 1 (0.00 confls per restart)
c blocked restarts : 0 (0.00 per normal restart)
c decisions : 0 (0.00 % random)
c propagations : 0
c decisions/conflicts : 0.00
c conflicts : 0
c conf lits non-minim : 0 (0.00 lit/confl)
c conf lits final : 0.00
c cache hit re-learnt cl : 0 (0.00 % of confl)
c red which0 : 0 (0.00 % of confl)
c props/decision : 0.00
c props/conflict : 0.00
c 0-depth assigns : 2 (0.00 % vars)
c [occ-substr] long subBySub: 0 subByStr: 0 lits-rem-str: 0
c [scc] new: 0 BP 0M T: 0.00
c Conflicts in UIP : 0
c Mem used : 0.00 MB
v -1 -2 3 4 0
First, there is an analysis of how the solver worked. The very last line is the most important. It is the line v -1 -2 3 4 0. The v tells us that an answer was found. This is a verified correct solution.
The result line then tells us how to set the variables. It says v -1 -2 3 4 0. Any number with a minus sign needs to be set to False. Any number without a negative sign needs to be set to true.
This is telling us
Variable |
DiMACs Result |
Value |
|---|---|---|
A |
-1 |
False |
B |
-2 |
False |
C |
3 |
True |
X |
4 |
True |
We can verify this is a correct answer. A SAT Solver provides one answer, but there may be many correct answers.
We can run the expression in Racket to see it evaluates to true.
#lang racket
(define A #f)
(define B #f)
(define C #t)
(define X #t)
(and (or (not A) (not B))
(or (not C) X)
C
);#t
There are many SAT Solvers for different languages. Python has PySAT. Racket has an entire package Rosette for working with logic problems. There are also simple solvers like SAT.rkt for simple problems.
