Proof by Deduction

Logical Deduction is a method of formalizing the process of drawing conclusions from a set of premises.

You are read more at the links below

• Deductive Reasoning on Wikipedia

• For All X from Open Logic Project

We will use a Proof Checker Website. This will allow you to check that all your steps are correct and you reach the correct conclusion.

Logical Deduction

A premise is a statement that is known to be true at the start of the deduction. We assume these facts are true. Deduction is the process of deriving new conclusions based on our premises and the rules of logic.

Let us assume that all men are mortal. Let us further assume that Socrates is a man. These are our two premises. We can then conclude that Socrates, since he is a man, must also be mortal. We combined the information from our premises to learn something new.

1. All men are mortal

2. Socrates is a man

3. Socrates is mortal

We often use chained conditionals. Larry is a student in a class. If he gets sick, then he will be absent from class. If he is absent from class, then he will miss his classwork. These are our new premises. We realize that these combine to tell us that if Larry is sick, then he will miss his classwork.

1. If Larry is sick, then he will be absent.

2. If Larry is absent, then he will miss his classwork.

3. If Larry is sick, then he will miss his classwork.

These makes sense, but is not formal. It requires human intuition to figure out the new statements based on the premise. We want to formalize this into something that has a fixed set of rules. That way everyone can convey information in a consistent manner. With a formal set of rules, we can also verify the deduction. This way we can ensure no mistakes are made, we could even automate some deductive proofs.

A deductive proof starts with any premises. These are things we assume to be true within the proof. If they are true in practice is not part of the deduction. We just work under the assumption they are true. Our proof is only correct if the premises are actually true. If the premises turn out to be false, the proof is worthless.

The last line of the proof is the conclusion. This is what we are proving is true because of the premises. In between, we use the Laws of Deduction to get from the premises to the conclusion.

The “thing” we a proving is called an argument. An argument is a set of premises followed by a conclusion. The proof verifies that the conclusion must be True if the premises are true.

Argument’s have a fixed format. A general template is given below.

\( \begin{align} \phi_1, \phi_2, \cdots, \phi_3 \therefore \psi \end{align} \)

The premises are separated by commas. These are shown as \(\phi_n\) above. The therefore symbol \(\therefore\) is used to denote the conclusion. There is only one conclusion at the end of the of premises. In this example, the placeholder for the conclusion is \(\psi\).

Let us return to the example from earlier, but add variables to the statements.

• \(S\) is true when Larry is sick.

• \(A\) is true when Larry is absent.

• \(C\) is true when Larry completes his classwork.

We can rewrite each sentence as a logical expression.

• \(S \implies A\) means “If Larry is sick, then he will be absent.”

• \(A \implies \neg C\) means “If Larry is absent, then he will miss his classwork.”

• \(S \implies \neg C\) means “If Larry is sick, then he will miss his classwork.”

We can write this as an argument.

\( \begin{align} (S \implies A), (A \implies \neg C) \therefore (S \implies \neg C) \end{align} \)

Once we have an argument, we need to use a proof to verify it is true.

Basic Deductive Rules

The Rules of Deduction are built around the Boolean operators we have already seen. Deduction is a kind of logical reasoning. We will start with rules related to three Boolean operations. We will introduce the negation in the next sections. Using the negative operator in proofs adds a significant level of complexity.

As we saw with truth tables, we can make up and prove any rules we want. This may be useful in some contexts, but it can also prove problematic. If everyone is using different rule sets, it is hard to communicate proofs. The Rules of Deduction provide a small, complete, and consistent set of rules that can be used in proofs.

Note

The basic Rules of Deduction are complete in the sense that they can be used to prove anything that could be proven by a truth table. Since all boolean algebra statements can be proven by truth tables, the Rules of Deduction are exactly as powerful as truth tables.

We will start with the rules for conjunctions, disjunctions, and conditionals. Each operator has a rule to introduce a new operator into the proof. It also has an elimination rule that removes the operator from the proof.

Operation	Add Operator	Remove Operator
\(\wedge\)	Conjunction Introduction	Conjunction Elimination
\(\vee\)	Disjunction Introduction	Disjunction Elimination
\(\implies\)	Conditional Introduction	Conditional Elimination

We will introduce the rules based on their complexity to use.

Conjunction Introduction

If we have two statements that are true, we can say they are both true together. Imagine it is a rainy day. You could look outside and verify the premise Rainy=True. Next, you look at the calendar at see it is Wednesday. You have verified the premise Wednesday=True. The rule of Conjunction Introduction states that you can say

It is a rainy day and a Wednesday.

You verified both premises independently, you are now allowed to use a conjunction to say they are both true together.

In deduction, we are proving an argument. The argument has two sides. The first is the list premises. The second is a conclusion.

We can formally write the above argument. Let \(R\) be a Boolean variable that is true when it is rainy. Let \(W\) be a Boolean variable that is true when it is Wednesday. We are making the argument that if both premise are verified independently, we can state that it is rainy and Wednesday.

The argument is formally written as

\( \begin{align} R, W \therefore R \wedge W \end{align} \)

When writing a proof, every statement except the premises must be justified by a rule. The premise is justified by stating that it is a premise. In these examples, we will specific the premise in our proofs. Sometimes a premise just has no justification written at all.

Our first rule is Conjunction Introduction. This rule states that if two lines are true, we may combine the two lines using the conjunction operator. The justification is written in shorthand as \(\wedge I\). It is followed by the line numbers where the two sides of the conjunction are justified. Anyone who wants to verify the proof can look at those line numbers and check that they both sides of the conjunction are true.

The proof is shown below.

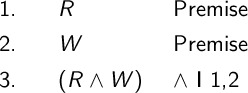
This proof justifies the argument \(R,W \therefore (R \wedge W)\).

If we know that \(R\) is true and \(W\) is true, we know that \(R \wedge W\) must also be true. If it isn’t Wednesday, this proof is still correct. We just can’t use it for anything since the premise is False on that day. The proof is always correct, but it is only useful when the premises are all true.

Note

Just because a proof is true, does not mean the argument is useful for anything. Conceptually, we could prove that if cakes were intelligent then it would be wrong to eat cakes. It may be possible to prove this argument. Regardless, cakes are not intelligent. We can’t actually use the proof in real life. It just because a thought exercise.

In the proof, the right side of the each step specifies which rules was used. The first two lines are premises and assumed to be true. The \(\wedge I\) says we are using the Conjunction Introduction rule. The two numbers tells us which lines of the proof the two inputs came from (Lines 1 and 2). The order in which the two numbers are written does not matter.

Disjunction Introduction

If we want to introduce the disjunction operator, we need to know one of the two sides is true. Let us again imagine a rainy day. We know for a fact it is rainy out. It would be true to say

It is rainy or Monday today.

It doesn’t matter at all if it is actually Monday. We know it is rainy, therefore the statement is true.

The argument we are proving is \(R \therefore (R \vee M)\). The justification we going to use is disjunction introduction. This justification only needs to cite one line. We need to know one of the two sides is true and cite that line.

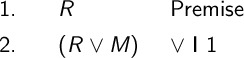
If we know that \(R\) is true, we can draw the conclusion that \(R \vee M\) is true. Note that \(M\) has never appeared in the proof up till now. It is a completely new variable. We can add anything with Disjunction Introduction. We just need to know half the expression must be true.

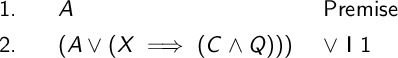
This is true because the argument is really just an implies.

\( \begin{align} R \implies (R \vee M) \end{align} \)

The truth table for this expression is as follows

\(R\)	\(M\)	\(R \implies (R\vee M)\)
T	T	T
T	F	T
F	T	T
F	F	T

If we know \(R\) is true because it is a premise, the value of \(M\) doesn’t matter. This is covered by the first two lines of the truth table.

The justification for Disjunction Introduction only takes one line number, the half of the disjunction that is known to be true.

Conjunction Elimination

Conjunctions can also be eliminated. Since we know both sides of the conjunction must be true, we can determine that either side is true independently.

It is snowing and windy.

You can draw the conclusion that it is snowing. The windy part might not be relevant to your life. If we know a conjunction statement is true, then its two parts must also be true. We can prove that it is snowing by discarding the windy part of the clause.

We can prove that \(S \wedge W \therefore S\).

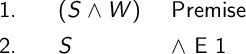
The justification is \(\wedge E\) followed by the line number containing the conjunction.

We can prove the commutative property of the conjunction operator using the rules we have seen so far. We will prove \((A \wedge B) \therefore (B \wedge A)\).

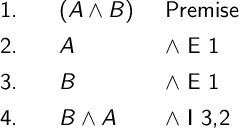
To fully justify the commutative property we need to also provide a proof in the opposite direction \((B \wedge A) \therefore (A \wedge B)\).

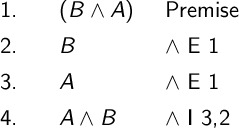
With both these proofs, we know that \((A \wedge B) \iff (B \wedge A)\). The commutative property is justified by deduction. We can only state equivalence (bi-conditional) if we can do a proof in both directions.

Conditional Elimination

What if our premises contain a conditional statement? We are told ``if it rains then it pours’’. We verify that it is raining. We can draw the conclusion that it is pouring.

The argument we are making it \((R \implies P), R \therefore P\). The proof is given below.

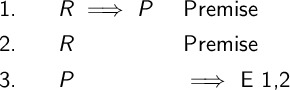
If we know that an implies is true and we know the left side is true, we can draw the conclusion that the right side must be true. The justification symbol is \(\implies\) E. It requires two line numbers. One is the conditional statement itself. The other is the line justifying the left side of the implies. Once we know the left side is true, we can conclude the right side is true. Remember, the implies is false when \(T \implies F\). If we know the implies is true, this situation is impossible.

Conditional Introduction

What if we want to make an assumption? This happens in a subproof. We imagine a world in which something is true, even though we have not verified it. We can use rules in this imaginary world to justify arguments. We can then draw conclusions from the subproof.

You have probably seen this already in mathematics. We write things like “let us assume x is even”. We aren’t verifying \(x\) is even, we are just pretending it is true for our proof. We can make these kinds of assumptions in our deductive proofs.

One case where we need assumptions is to create a new conditional. This rule is called conditional introduction.

What if we want to prove that if \(A\) is true then \(B\) will be true. We might not actually know if \(A\) is true or not. We can assume it is. We are only trying to prove a conditional statement. We can use this rule to finally prove our argument about Larry from earlier.

1. If Larry is sick, then he will be absent.

2. If Larry is absent, then he will miss his classwork.

3. If Larry is sick, then he will miss his classwork.

We can create variables again.

• \(S\) is true when Larry is sick.

• \(A\) is true when Larry is absent.

• \(C\) is true when Larry completes his classwork.

The argument is \((S \implies A), (A \implies \neg C) \therefore (S \implies \neg C)\). We don;’t care if Larry is sick or not. We just want to know what happens if he is sick. We just assume he is sick and see what happens.

The proof is written as follows

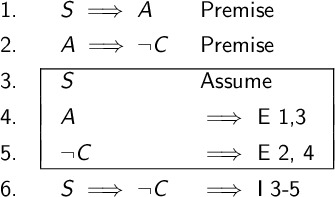
The subproof is draw with a special box or symbol. This tells the reader that the lines in the subproof only work because of the assumption. It is an imaginary world where \(S\) is true. The first line is only justified by assume. There is no verification this statement is true, we are just pretending it is in the box. Sometimes, this is left out and the first line is just implied by the reader to be the assumption.

This subproof is justifying a conditional statement. We said “assume S is true” and that lead us to the subproof’s conclusion \(\neg C\) is true. In our imaginary world, we know \(\neg C\) is true.

The shorthand name for the justification is \(\implies I\). It requires a range of numbers. The entire subproof starting at line 3 and ending at line 5 is the justification.

When we leave the imaginary world of the subproof, we still have no idea if \(S\) is true or not. We can still draw one conclusion that is valid in the real world \(S \implies \neg C\). If Larry is sick, then he will miss classwork. We have used our subproof to justify a conditional that is true in our argument.

Disjunction Elimination

What if we want to take apart a disjunction statement? If a disjunction is true, it could be for multiple reasons. Either of the two inputs could be true and the other false. The could also both be true.

To break apart a disjunction, we need to make two assumptions and see what happens. If we know a disjunction, \(A \vee B\) is true, we have no way to know which of the two values made it true. We have to assume both sides are true and see what happens in each case. If both reach the same conclusion, then we can say that conclusion is true in the argument. It doesn’t matter which side of the disjunction caused it, because both lead to the conclusion.

The subproof based in the assumptions is again drawn in a box. We prove the argument \((A \implies X), (B \implies X), (A \vee B) \therefore X\).

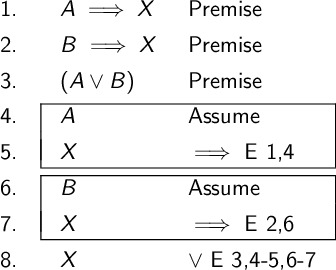
The disjunction elimination has the most complex justification we have seen so far. If both our imaginary worlds lead to the same conclusion, then it doesn’t matter which is true. Either leads to the correct conclusion.

The justification starts with the shorthand \(\vee\) E. We then provide the line justifying the disjunction is true. Next, we provide a subproof showing that if the left side of the disjunction is true then our conclusion holds. Finally, we provide a subproof for the right side. Both subproofs require a range of numbers with the entire subproof.

Proof Terminology

An argument is valid if it is impossible for the premises to be true and the conclusion to be false. Any complete proof by deduction makes the argument valid. An argument is invalid if there exists at least one case where the premises are all true by the conclusion is false. If a proof by deduction is completed correctly, it’s argument cannot be invalid.

Remember, we never actually verify the premises in our proof. A proof can be valid and the premise can still be wrong. An argument is sound if the proof is valid and the premises are confirmed to be true.

Examples

Below are some additional example proofs by deduction.

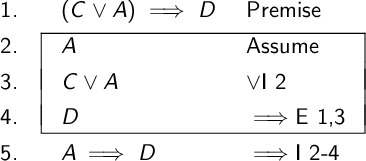
Argument: \(((C \vee A) \implies D) \therefore (A \implies D)\)

Argument: \((\neg K \implies M), (N \implies M), (\neg K \vee N) \therefore (M \vee R)\)